The bound charge density is given by
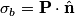 where 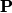 is the polarization vector in the dielectric and is the polarization vector in the dielectric and 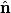 is a normal vector that points from the dielectric to the conductor. The polarization vector in the dielectric is is a normal vector that points from the dielectric to the conductor. The polarization vector in the dielectric is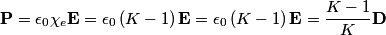 The electric displacement produced by the charge density 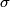 is is 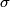 , and it is in the direction opposite , and it is in the direction opposite 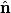 . Thus, . Thus,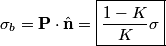 Therefore, answer (E) is correct. |